Crotosolve

For my bachelor’s thesis at the Karlsruhe Institute of Technology (KIT), I had the pleasure to work on a research project with Dr. Eileen Kühn, Dr. Max Fischer and Prof. Achim Streit. Their lab at KIT’s Scientific Computing Center had stumbled upon a neat property of univariate parameter changes in parameterised quantum circuits (PQCs). Namely, plotting the expectation value of any measurement after a PQCs w.r.t. a single parameter used in a Pauli rotation gate will always produce a (possibly shifted and scaled) sine function. This characteristic was also discovered earlier by Ostaszewski et al. and used for a univariate optimisation algorithm called Rotosolve, which evaluates the PQC three times to reconstruct the sine function and compute the optimal parameter value, for each parameter.

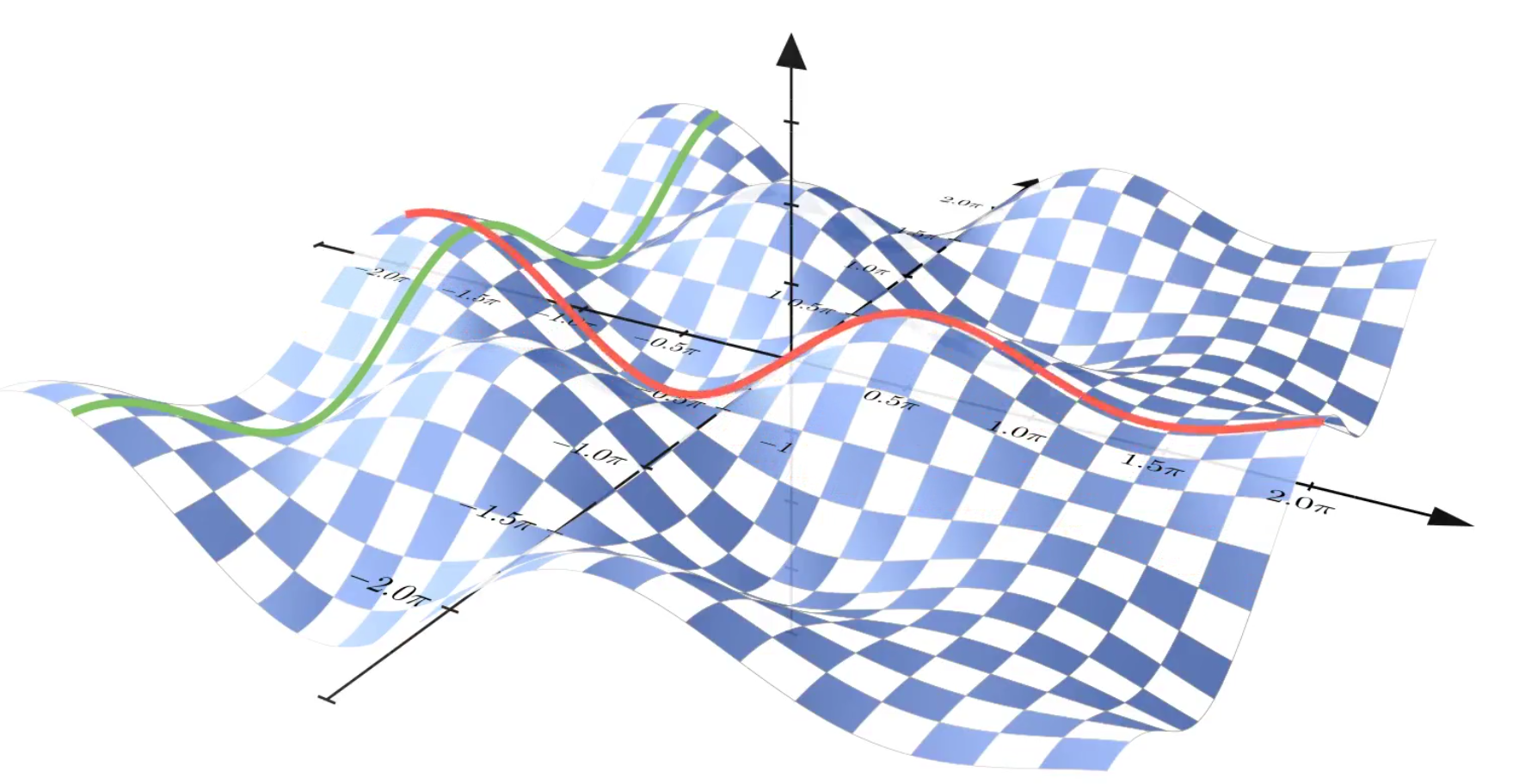
Fig. 1: The expectation value of a measurement is plotted w.r.t. two parameters for Pauli rotation gates. The green and red lines demonstrate that both expectation values have an univariate, sinusoidal dependency on the parameters.

The original approach based on the sine shape was limited to optimising PQCs where each parameter is used in one Pauli rotation gate. However, another commonly used gate in PQCs is the controlled Pauli rotation gate which spans two qubits. A parameter used in this type of gate no longer produces a sinusoidal expectation function but a $4\pi$-periodic wave-like function.

The goal for my bachelor’s thesis was to characterise this type of function and to develop an extension to the Rotosolve algorithm that could handle both regular Pauli rotation gates and controlled ones. Indeed, the expectation value function of controlled Pauli rotation gates is a superposition of two sine waves with different speeds which can be characterised by five scalar values. My Rotosolve extension — called Crotosolve — can reconstruct these functions from five PQC evaluations and leverage onedimensional, numerical optimisation algorithms to compute the (univariately) best parameter value. Compared with Rotosolve and standard quantum machine learning optimisers, Crotosolve consistently exhibits comparable or better loss curves on a PQC benchmark¹.

• 📖 Read my bachelor’s thesis
• 🆓 Check out the data and source code on GitHub or Zenodo

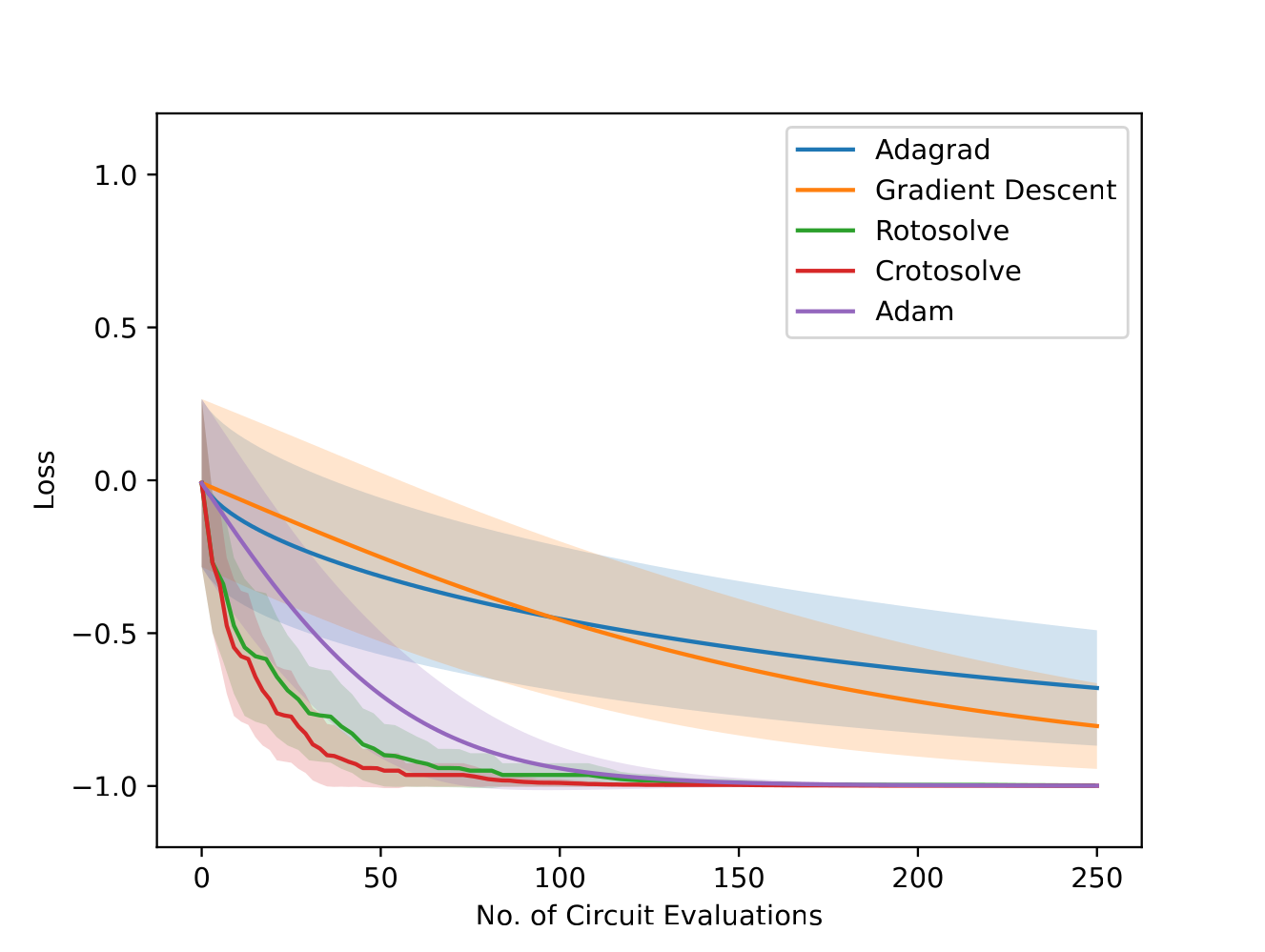
Fig. 2: Various optimizers minimize the expectation of a PQC with four qubits and three layers. Full lines show the average loss curve. Transparent areas show the error, which is the average ± its standard deviation.

Footnotes

1. It should be noted that the performance of QML optimisers can often be improved through hyperparameter tweaking. Here, we only consider these optimisers with their default values and highlight that Crotosolve works well and consistently out of the box. The benchmark is based on a PQC library proposed by Sim et al. and all evaluation details are presented in Section 5.2 of the thesis. ↩