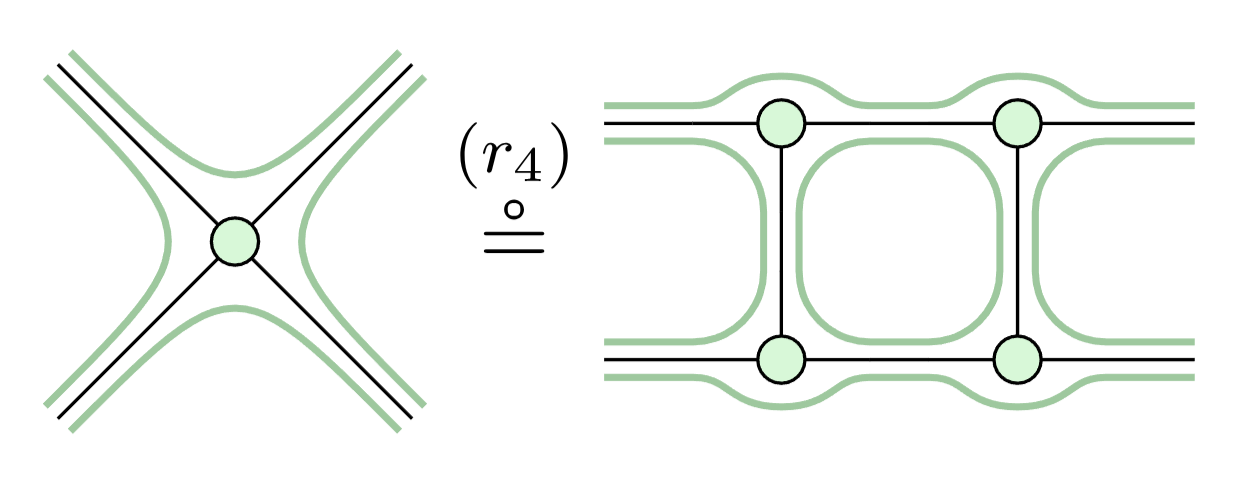
Fig. 1: A matchability-preserving decomposition of a four-legged
spider.
For my master’s dissertation project in Oxford, I worked with Prof. Aleks Kissinger, his PhD student Benjamin Rodatz and Dr. Linnea Grans-Samuelsson to understand the impact of ZX rewrites on efficient decoding in Quantum Error Correction (QEC). Our original idea for the project was to characterise when ZX rewrites make the decoding problem of the circuit’s spacetime code more difficult and when the decoding problem becomes easier. After exploring the problem for a while, we narrowed down the project’s scope to the Minimum Weight Perfect Matching (MWPM) case, one of the most well-researched efficient decoders in QEC.
My thesis “Preserving MWPM Decodability in Fault-Equivalent Rewrites” first develops detector-aware rewrites to track how ZX rewrites can affect the decoding problem. Combining this novel notion with fault-equivalent rewrites allows us to define matchability-preserving rewrites which guarantee to keep MWPM Decodability intact throughout quantum compilation. And indeed, we found a system of such rewrites that we can use to build implementations for arbitrary surface code measurements.
Full Dissertation Abstract
For the successful application of quantum computers, the suppression of noise has often been dubbed as the most critical problem. Quantum Error Correction (QEC) codes encode the state of logical qubits onto a higher number of physical qubits, adding reduncancy to make limited amounts of noise detectable and correctable in theory. However, computing the right correction for a given syndrome is generally -complete. Yet, corrections must be performed at a high frequency to suppress noise successfully. For the surface code, the decoding problem is guaranteed to have a specific structure that enables efficient decoding through the Minimum-Weight Perfect Matching (MWPM) decoder. This property can be lost when constructing implementations for the detector measurements, making the decoding problem hard again.
In this work, we take a circuit-centric perspective to define matchability-preserving rewrites. Based on the ZX calculus and the recently introduced fault-equivalent rewrites, we formalise how the decoding problem changes through the application of ZX rewrites to a given diagram and detector basis. This allows us to analyse whether given ZX rewrites preserve the property that enabled efficient MWPM decoding. We demonstrate a set of matchability-preserving rewrites that can be used to build fault-tolerant syndrome measurements for surface codes.
— Abstract of my master’s thesis